SISTEMAS DE ECUACIONES LINEALES
Sistemas de Ecuaciones:
Métodos de resolución
En esta página vamos a exponer los 3 métodos básicos para resolver sistemas de ecuaciones lineales: sustitución, reducción e igualación. Para facilitar la comprensión de los métodos, sólo vamos a resolver sistemas de 2 ecuaciones con 2 incógnitas.
Cuando sepamos resolver un sistema, ya podemos resolver problemas de aplicación: Problemas de sistemas.
Recordatorio:
El coeficiente de una incógnita es el número que la multiplica. Por ejemplo,
el coeficiente de 2x es 2,
el coeficiente de x es 1,
el coeficiente de -x es -1.
Explicaremos los métodos con 4 pasos y mediante un ejemplo.
1. Método de Sustitución
El método de sustitución consiste en aislar en una ecuación una de las dos incógnitas para sustituirla en la otra ecuación.
Este método es aconsejable cuando una de las incógnitas tiene coeficiente 1.
Ejemplo 1
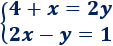
1. Aislamos una incógnita
Vamos a aislar la x de la primera ecuación. Como su coeficiente es 1, sólo tenemos que pasar el 4 restando al otro lado:
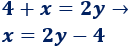
Ya tenemos aislada la incógnita x.
2. Sustituimos la incógnita en la otra ecuación
Como tenemos que la incógnita x es igual 2y-4, escribimos 2y-4 en lugar de la x en la segunda ecuación (sustituimos la x):
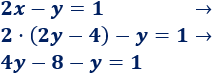
Observad que hemos utilizado paréntesis porque el coeficiente 2 tiene que multiplicar a todos los términos.
3. Resolvemos la ecuación obtenida:
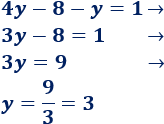
Ya sabemos una incógnita: y=3.
4. Calculamos la otra incógnita sustituyendo:
Al despejar la incógnita x teníamos

Como conocemos y=3, sustituimos en la ecuación:
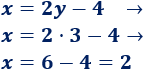
Por tanto, la otra incógnita es x=2.
La solución del sistema es
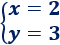
2. Método de Reducción
El método de reducción consiste en sumar (o restar) las ecuaciones del sistema para eliminar una de las incógnitas.
Este método es aconsejable cuando una misma incógnita tiene en ambas ecuaciones el mismo coeficiente (restamos las ecuaciones) o los coeficientes son iguales pero con signo opuesto (sumamos las ecuaciones).
Ejemplo 2
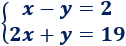
1. Comprobamos los coeficientes
Hay que asegurarse de que al sumar o restar las ecuaciones, alguna de las incógnitas desaparece:
Escogemos una incógnita a eliminar: la y.
Sus coeficientes son -1 (en la primera) y 1 (en la segunda).
Como son iguales y de signo contrario, sumaremos las ecuaciones.
Nota: si ninguna de las incógnitas tiene el mismo coeficiente, podemos multiplicar cada ecuación por el número distinto de 0 que sea necesario para conseguirlo. Un ejemplo de esto lo podemos encontrar en el Problema 2.
2. Sumamos o restamos las ecuaciones
Sumamos las ecuaciones para eliminar la y:
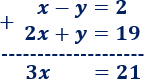
3. Resolvemos la ecuación obtenida
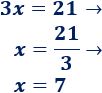
4. Calculamos la otra incógnita sustituyendo
Sustituimos la incógnita x por 7 en alguna de las ecuaciones y la resolvemos:
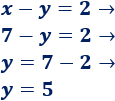
La solución del sistema es
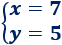
3. Método de Igualación
El método de igualación consiste en aislar una incógnita en las dos ecuaciones para igualarlas.
Este método es aconsejable cuando una misma incógnita es fácil de aislar en ambas ecuaciones.
Ejemplo 3
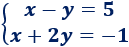
1. Aislamos una incógnita en las dos ecuaciones
Escogemos aislar la incógnita x:
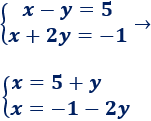
2. Igualamos las expresiones
Como x=x, podemos igualar las expresiones obtenidas:

3. Resolvemos la ecuación
Resolvemos la ecuación de primer grado obtenida:
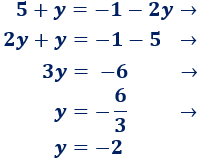
4. Calculamos la otra incógnita sustituyendo
Sustituimos el valor de la incógnita y en alguna de las expresiones calculadas anteriormente (la primera, por ejemplo):
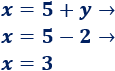
La solución del sistema es
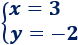
Más Sistemas Resueltos
Problema 1
Resolver el siguiente sistema por el método de igualación:
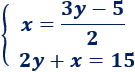
1. Aislamos la incógnita x en la segunda ecuación (en la primera ya está aislada)
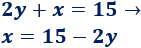
2. Igualamos las expresiones
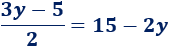
3. Resolvemos la ecuación
El 2 del denominador pasa al otro lado multiplicando:
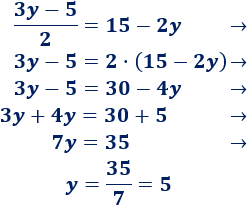
4. Calculamos la otra incógnita sustituyendo el valor de la incógnita y en la primera ecuación
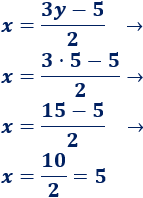
La solución del sistema es
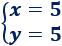
Problema 2
Resolver el siguiente sistema por el método de reducción:
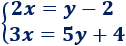
1. Comprobamos los coeficientes
Vamos a eliminar la incógnita x. Su coeficiente en la primera ecuación es 2 y en la segunda ecuación es 3. Para solucionar esto, multiplicamos la primera ecuación por 3 y la segunda por 2:
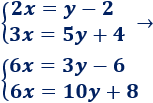
Ahora, la incógnita x tiene el mismo coeficiente en ambas ecuaciones.
2. Restamos las ecuaciones
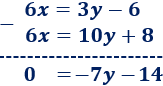
3. Resolvemos la ecuación obtenida
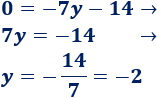
4. Calculamos la otra incógnita sustituyendo en la primera ecuación
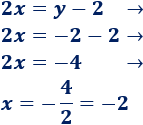
La solución del sistema es
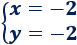
Problema 3
Resolver el siguiente sistema por el método de sustitución:
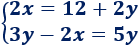
1. Aislamos la incógnita x en la primera ecuación
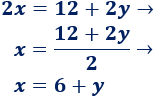
2. Sustituimos la incógnita en la otra ecuación
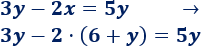
Nota: No olvidéis escribir el paréntesis al sustituir.
3. Resolvemos la ecuación obtenida
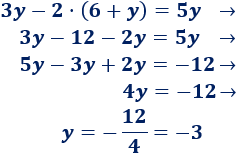
4. Calculamos la otra incógnita sustituyendo
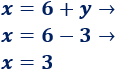
La solución del sistema es
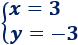
Comentarios
Publicar un comentario